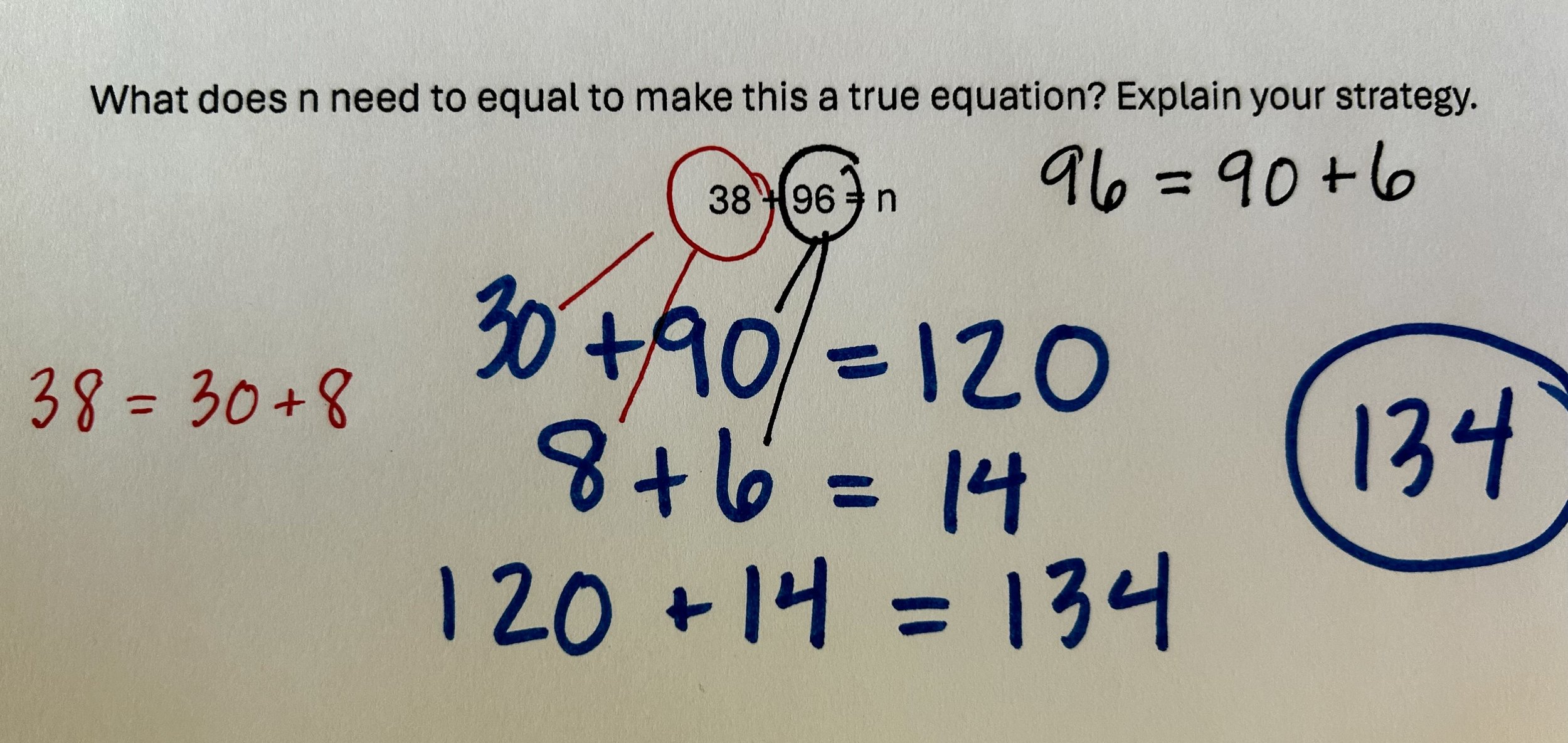Using “Express” Rather Than “Decompose” with Elementary School Students by Linda Levi

Elementary school teachers  often use the word “decompose” with their students. For example if Duane explained his strategy for the problem, 7 + 9 = n, as, “I know that 7 + 3 is 10 and then 6 more is 16” his teacher might write the following and say,

“Who can explain how Duane decomposed 9 when solving this problem?” If a student replied, “He decomposed 9 into 3 and 6”; the teacher would conclude that this student understood how Duane thought of 9 when solving this problem.

The word “decompose” matches how Duane thought of 9 when solving this problem.

Now consider how Duane’s classmate Jade solved the problem 7 + 9 = n. She explained her strategy as, “I know that 7 + 10 is 17. 9 is 1 less than 10 so I subtracted 1 to get 16.” This student thought of 9 as 10 minus 1 to solve the problem.  An adult can understand that 9 was decomposed into 10 and -1, but most elementary school students wouldn’t associate the term decompose with how Jade thought of 9 when solving this problem.

Dr. Jae Baek, Assistant Professor at Illinois State University, introduced me to using the word, “express” rather than “decompose” for describing how students think of a quantity in a different way when solving a problem.

For example, after hearing Jade describe her strategy in a one-on-one interaction, her teacher might write the following And say, “Let me make sure I understand your strategy. You expressed 9 as 10 minus 1, and then added 10 to get 17, and then subtracted 1 to get 16.”

Alternatively, Duane’s teacher could have said, “You expressed 9 as 3 + 6 and first added 7 and 3 to get 10, and then added 6 to get 16.”

Using “express” fits with thinking of a quantity as a sum as well as a difference. Express also works when thinking of a quantity as a product or quotient.

Dr. Baek stated another advantage of using the term express is setting a foundation for elementary school students to understand the term “expression” as it is used throughout middle school, high school and college mathematics. I never used the word “decompose” when teaching high school math, nor have I seen “decompose” in high school or college math textbooks.

Here is a classroom vignette where the teacher uses the term express with his students. Since we learn vocabulary by hearing it in context,  Mr. A says uses the word “express” without formally defining it. The students have solved the problem 38 + 96 = n and Mr. A is leading a discussion of their strategies.

Mr. A: We are going to discuss some strategies that you used when solving the problem, 38 + 96 = n. Here is how one of your classmates solved the problem. Mr. A: Discuss with your partner how you think this student solved the problem.

After 2-3 minutes, Mr. A brought the class back together.

Mr. A: How do you think this student solved the problem? Jordan?

Jordan: First, they added 30 plus 90 and got 120.

Mr. A: Where did the 30 and 90 come from?

Jordan: The 30 came from the 38 and the 90 from the 96.

Mr. A: Ok, let’s start by thinking about the 30 coming from the 38. How did this student think of 38? Tyrone?

Tyrone: 38 is 30 and 8

Mr. A: When you say the word “and” Tyrone, is there an operation that you are thinking about like addition, subtraction, multiplication or division?

Tyrone: Addition. 

Mr. A: 38 is the same as 30 + 8, do people agree? (general agreement) So this student expressed 38 as 30 + 8 when solving this problem.

Mr. A: How did this student think of 96? Another way I could ask this question is, how did this student express 96? Discuss with your partner how this student expressed 96.

After a minute, Mr. A brought the class back together.

Mr. A: Aliah, how did you and your partner think this student expressed 96?

Aliah: 90 and 6

Mr. A: Could you use a math term rather than the word and?

Aliah: 90 plus 6.

Mr. A wrote the following

Mr. A next had students examine the strategy on the right and discuss with their partners how they thought this student solved the problem.

Mr. A: Does anyone have a conjecture about how this student solved this problem? Josue?

Josue: They added 100 and then took away 4.

Mr. A: Why do you think they did that?

Josue: 96 is close to 100, it’s only 4 away. They added 100 and then they took those extra 4 away.

Mr. A: How did this student think about 96 in this problem? Discuss this question with your partners. 

Mr. A listened while students discussed this question and noticed that Tylesha said that 100 – 4 = 96. Mr. A doesn’t always call on the student who will give him the answer he is looking for, but since he was introducing the term express today, he decided to call on Tylesha.

Mr. A: Tylesha, I overheard you share how you thought that this student thought of 96 in this problem.

Tylesha: First, I was thinking 96 + 4 = 100 but then I thought, you asked how they thought of 96, so it’s 96 = 100 – 4

Mr. A wrote the following

Mr. A: Tylesha thinks that this student expressed 96 as100 – 4. Talk with your partners about whether you agree.

The class continued to discuss this strategy. In this example, the student didn’t express 38 in any way other than 38. Within a couple weeks of Mr. A using the term express with his students, they started using it on their own.

Here are a few more examples of how teachers could use the term express when describing students’ strategies

In this example, the student expressed 5/6 as 5 × 1/6 when solving this problem. They didn’t express 42 in any way other than 42.

In this example, the student expressed 5/6 as 1 – 1/6.

In this example, the student expressed 25 as 100 ÷ 4. First, they multiplied by 100 and then they divided by 4.

In this example, the student expressed ¾ as 3 ÷ 4.  First, they divided by 4 and then they multiplied by 3.

I encourage you to experiment with using express rather than decompose  when students are solving problems by thinking of a quantity in a way differently than it is stated. It will instill a foundation for understanding of the term “expression” in their future years of education.